谷宗喜1， 徐安军1*， 贺东风1， 吴 伟2， 刘晶波2， 韩伟刚3
(1. 北京科技大学冶金与生态工程学院，北京 100083；2. 重庆钢铁集团股份有限公司，重庆 401258；3. 钢铁研究总院先进钢铁流程及材料国家重点实验室，北京 100081)
摘 要：在综合考虑铁水包备包生产及高炉配罐制度等因素的基础上，建立了多功能铁水包周转数计算模型，即铁水包周转数由工艺要求数、备包数及高炉配罐富裕数组成. 依据模型计算出重钢新区两座高炉-两座转炉模式下铁水包周转数为16 个. 结果表明，减少铁水包周转数的关键在于减少重包和空包的“缓冲容量”，为此需优化高炉配罐制度及连浇炉数. 单一优化配罐制度及连浇炉数均可减少2 个铁水包，联合优化配罐制度和连浇炉数可减少4 个铁水包.
关 键 词：铁水包；周转数；计算模型；缓冲容量
1 前 言
多功能铁水包模式，即“一包到底”模式，是指高炉(Blast Furnace, BF)出铁、铁水运输、铁水预处理及向转炉(Basic Oxygen Furnace, BOF)兑铁均使用同一个铁水包，中途不倒包. 铁水包周转频率和周转数合理化研究是铁水包多功能集成技术包的重要研究内容[1]，首钢京唐[2]、重钢新区[3]等大型钢厂“铁钢界面”已经实施该技术，显示出良好的经济技术效果，但在生产运行中均存在周转数较多、周转时间较长等问题，影响“铁钢界面”动态有序运行. 从理论及实践角度均需解决合理调控铁水包周转数的问题. 多功能铁水包模式使原仅限于炼钢工序内部的全连铸生产组织管理延伸到了炼铁工序，铁水包周转过程受高炉出铁及连铸连浇等生产约束，目前针对铁水包(鱼雷罐)周转数的研究均未综合考虑各类约束条件对铁水包周转运行的影响，如供需平衡法[4]、排队论法[5]、仿真法[6]、基于生产计划的方法[7]等，目前尚未有新方法用于计算铁水包周转数[8]. 多功能铁水包周转过程与钢包周转过程类似，对多功能铁水包周转数及控制模型研究均较少[9]，对钢包的相关研究较多[10-14].本工作综合考虑铁水包周转过程备包生产及配罐制度等因素，以紧凑型“铁钢界面”布置的重钢新区为研究对象，建立了多功能铁水包周转数计算模型，提出减少铁水包周转数的生产措施，研究结果对多功能铁水包模式下合理配置铁水包周转数、加强铁水包周转运行管控均有一定的参考价值.
2 重钢铁水包周转过程解析
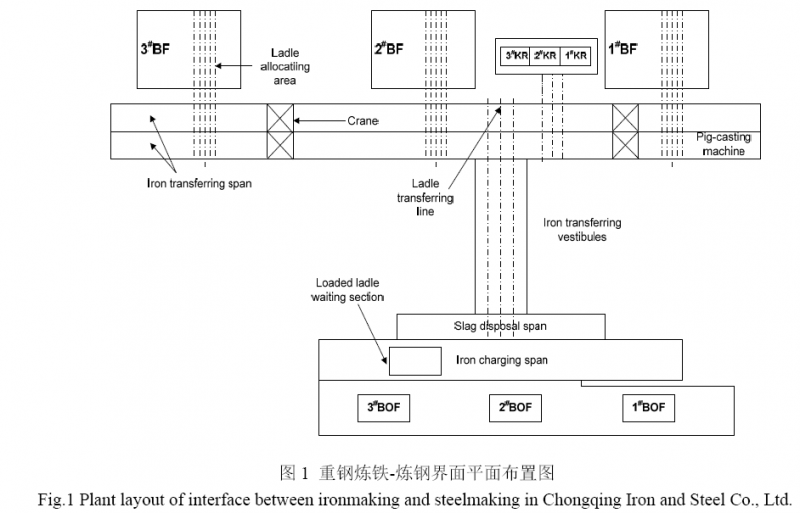
重钢“铁钢界面”目前有3 座高炉(1#~3#高炉均为2500 m3)、3 座KR(Kanbara Reactor)脱硫站和3 座230 t转炉，采用起重机+过跨车模式运送铁水包，图1 为其平面布置示意图，图2 为铁水包周转过程示意图，其中实线表示重包周转过程，虚线表示空包周转过程.
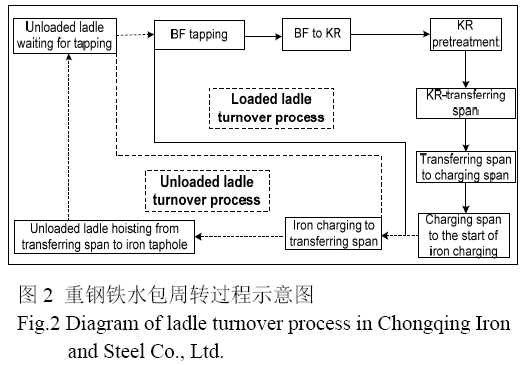
本工作提出用工艺要求时间表征铁水包周转过程中工序处理及转运必须时间，通过解析重钢铁水包周转过程，得出铁水包周转工艺要求时间如表1 所示，表中t1~t9 为铁水包周转各阶段工艺要求时间(min)，theavy 为重包周转工艺要求时间，包含出铁时间t1、出铁结束运输至KR 脱硫站时间t2、KR 脱硫时间t3、KR 脱硫结束至加料跨时间t4、加料跨吊起至兑铁时间t5、兑铁时间t6；tempty 为空包周转工艺要求时间，包含兑铁结束吊运至加料跨时间t7、加料跨至转运跨时间t8、转运跨至高炉出铁口时间t9. 由表1 可知，theavy=113 min，tempty=30 min.
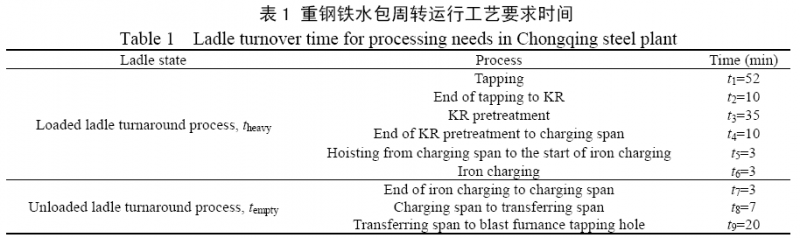
“一包到底”模式使原仅限于炼钢工序内部的全连铸生产组织管理延续到了炼铁工序，铁钢工序相互牵制，铁水包周转运行需保证高炉出铁安全及连铸连浇. 为保证高炉出铁安全，需考虑高炉配罐制度，即需在高炉出铁前预备若干数量空包[15]，重钢新区当前配罐制度为“3+1+X”，其中3 指3 个铁水包空包，1 为上一出铁批次的尾包，X 为依据高炉出铁波动需投入的铁水包个数，正常生产条件下，在每个出铁计划执行前，高炉出铁口均需准备3 个空包，上一个出铁计划剩余的尾包加入本次出铁计划. 为保证连铸连浇，需考虑铁水包备包生产，即需在转炉冶炼前保证适度的铁水囤积量[16]，目前两高炉-两转炉模式下，炼钢厂铁水积压到6 包时，应安排两条线同时生产，严禁炼钢厂积压铁水到8 包时不安排两条线同时生产.
3 铁水包周转数计算模型
通过对铁水包周转过程的分析可知，工序处理及铁水包转运时间一般较稳定，而备包及出铁前等待时间不固定，主要受冶炼计划和出铁计划影响. 基于以上分析，铁水包周转时间由工艺要求时间、备包时间及高炉出铁口前等待时间3 部分构成. 本工作提出铁水包周转数计算模型，即周转数由工艺要求数、备包数和配罐富裕数组成.
3.1 模型数学表达
模型假设条件：(1) 忽略高炉、预处理、转炉等工序生产波动，其中高炉每批次出铁包数固定，出铁连续进行，没有尾包，且高炉铁水无铸铁；(2) 铁水包转运时间稳定，波动较小；(3) 为方便建模，假设高炉与转炉一一对应；(4) 转炉与连铸工序炉机匹配，转炉冶炼时间随连铸浇注时间微调，炼钢计划开始时间不出现延迟；(5) 转炉冶炼计划间隔时间固定，由铁水包最长备包时间决定.
模型约束条件：(1) 铁水包备包数满足连浇需求；(2) 高炉出铁口前空包数需满足出铁计划需求.
模型数学表达式：
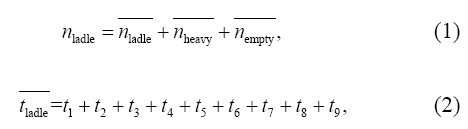
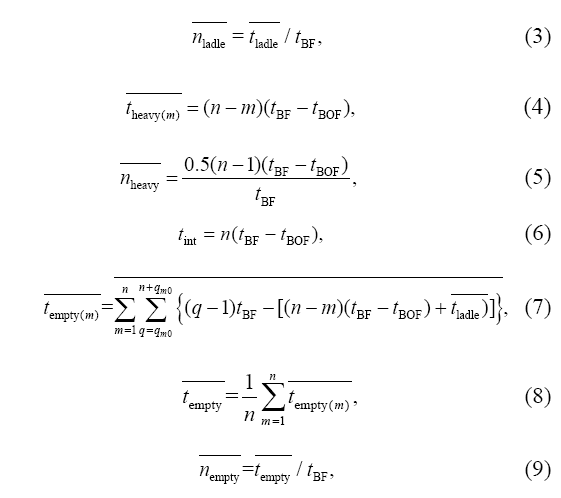
式中，nladle 为铁水包周转数(个)， 
为工艺要求周转数(个)， 
为必要备包数(个)， 
为配罐富裕数(个)，
为转炉两个冶炼计划间歇时间(min)，tBF 为高炉出铁时间(min)，tBOF 为转炉冶炼时间(min)，
为连浇炉数为n 转炉冶炼第m 炉时必要备包时间(min)，n 为连铸机连浇炉数，m 为转炉冶炼次序号(炉)，tint 为铁水包工艺要求时间(min)， 
为高炉第m 包铁水积压时间(min)，也是转炉冶炼计划炉数(炉)，q 为高炉第m 包铁水兑铁结束再次接铁的出铁序号，与备包时间和配罐制度有关，其中qm0 为铁水包初次投入接铁的出铁序号，
为铁水包到达出铁口至出铁前平均等待时间(min).
不同于钢包周转过程，铁水包周转过程必须保证高炉出铁安全，且多座转炉冶炼炉次重叠时间较长，铁水包几乎无互用现象，基本可认为多座高炉-多座转炉模式所需铁水包数等同于高炉-转炉“一一对应”模式所需包数之和[16,17]. 模型充分考虑了高炉出铁安全及连铸连浇需求，能较好描述铁水包实际周转过程.
3.2 模型应用
应用模型计算重钢新区铁水包周转数. 重钢高炉出铁平均时间tBF 为52 min，转炉冶炼时间44~50 min，冶炼时间参考后续连铸浇注时间微调. 选择1#、2#连铸机产能最大钢种AFT702 和BFT703，计算两高炉-两转炉模式下的铁水包周转数. 参考2013 年4~9 月生产数据，设定计算参数如表2 所示，其中连浇炉数取平均值.
按照模型分别计算1#高炉-1#转炉、2#高炉-2#转炉一一对应模式下铁水包周转数. 将表1 和2 相关参数带入式(2), (3), (5)，得到重钢新区当前铁水包周转数如表3 所示，依据模型绘制1#高炉-1#转炉铁水包周转运行甘特图如图3 所示，其中重包时间包含t1, t2, t3, t4, 
,t5，转炉兑铁时间为t6，空包时间包含t7, t8, t9, 
.
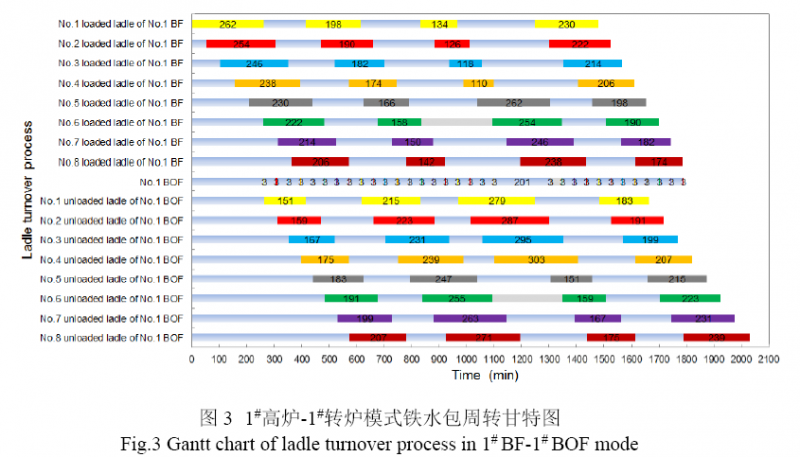
由表3 可知，重钢新区两高炉-两转炉模式下铁水包周转数为16 个. 由图3 可看出，铁水包周转过程呈现周期性循环的特点，重包备包时间
=0~152 min，
=76 min. 空包等待时间
=118~270 min，
=194 min，由此可知铁水包周转过程满足出铁安全需求.依照上述模式生产，高炉作业率为100%，转炉作业率为84.61%，实际生产中高炉作业率为97.19%，转炉为82.07%(2013 年4~9 月). 模型计算重钢新区两座高炉-两座转炉模式铁水包周转数为16，实际生产中考虑生产扰动等影响因素，铁水包周转数为19. 对比高炉与转炉工序作业率及模型计算与生产数据，可知所建模型与实际生产基本相符，可用于指导铁水包周转数的配置.
4 铁水包周转数量优化
多功能铁水包周转过程可认为是在“铁钢界面”循环运行的闭环串行生产线，考虑备包生产及高炉配罐，铁水包周转有两个关键的缓冲区，即空包缓冲区和重包缓冲区，“铁钢界面”生产组织的主要目的是尽可能减少铁水包等待数并保证“铁钢界面”生产连续运行[16].对于铁水包周转串行生产线，需分配合理的缓冲区容量以保证正常生产[17,18]. 实际生产中，工序处理及运输等工艺要求时间较稳定，优化铁水包周转数的关键在于减少高炉出铁口空包等待时间及备包时间，从而优化空包和重包缓冲容量.
4.1 空包缓冲容量的优化
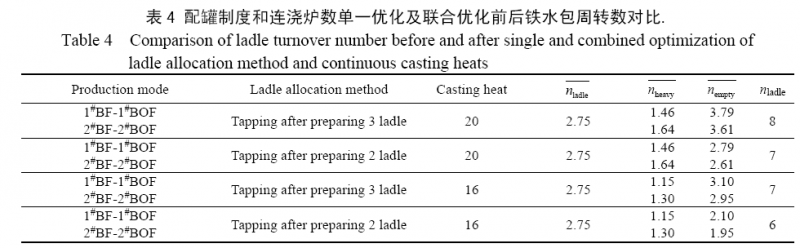
空包缓冲容量的优化应优化高炉配罐制度，实际生产中应将高炉空包配罐制度由“3+1+X”改为“2+1+X”，即在每个出铁计划开始前，高炉出铁口前空包数由3 减少为2. 优化配罐制度前后铁水包周转数量变化见表4.
4.2 重包缓冲容量的优化
重包缓冲容量的优化应合理安排炼钢计划，避免因炼钢计划延迟造成的不必要的备包，并选择合理的连铸机浇注周期和连浇炉数. 模型假定炼钢计划无延迟，即忽略由于炼钢计划延迟或不合理造成的备包数增加，且对于特定钢种其浇注周期基本固定，确定合理连浇炉数即可优化重包缓冲容量. 优化连浇炉数应从炼铁炼钢综合成本损失最小的角度核算，即计算由于铁水包备包造成的成本损失与炼钢综合成本损失，所得经济平衡点即为综合成本损失最低的连浇炉数. 重钢现场依据炼铁炼钢综合成本核算，针对典型钢种给出指导性建议，AFT702 和BFT703 的连浇炉数以15~16 炉为宜，优化的连浇炉数设为16 炉. 优化连浇炉数前后铁水包周转数量变化见表4.
4.3 结果分析
由以上分析可知，影响铁水包周转数量的关键因素为高炉配罐制度及连铸机连浇炉数，铁水包周转数量优化主要从优化配罐制度和连浇炉数两个方面采取措施.表4 为配罐制度和连浇炉数单一优化及联合优化前后铁水包周转数对比，依据模型绘制1#BF-1#BOF 模式联合优化铁水包周转运行甘特图如图4 所示.
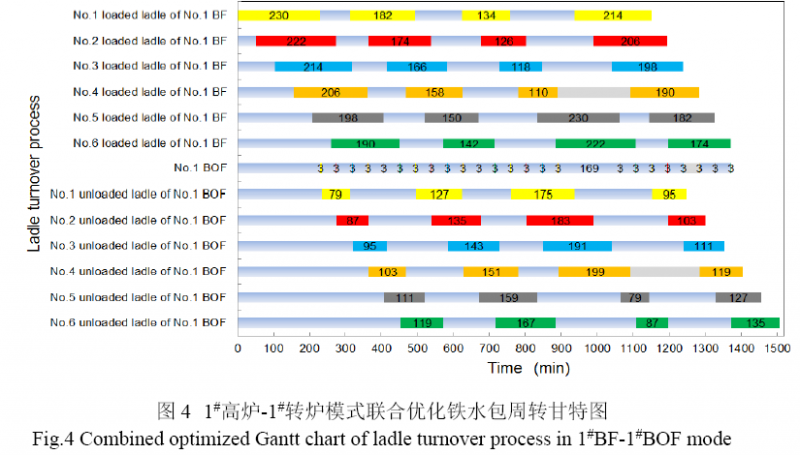
由表4 可知，配罐制度和连浇炉数单一优化时，两座高炉-两座转炉模式下铁水包周转数均可减少2 个；联合优化时，铁水包周转数量可减少4 个. 依据模型绘制单一优化及联合优化情况下铁水包周转运行甘特图，可知无论单一优化还是联合优化，铁水包均可满足高炉出铁及连铸连浇需求. 由图4 联合优化甘特图可看出，重包备包时间
=0~120 min， 
=60 min；空包等待时间
=46~166 min， 
=106 min，配罐制度和连浇炉数联合优化与未优化前相比，
减少16 min，
减少88 min.
减少铁水包周转数，需一方面优化高炉配罐制度，减少空包缓冲容量，即减少高炉出铁口空包等待数；另一方面需合理设定炼钢计划，合理选择连铸机浇注周期和连浇炉数，减少重包“缓冲容量”，即减少铁水包备包数.
5 结 论
针对多功能铁水包模式下铁水包周转运行须满足高炉出铁及连铸连浇等生产约束的生产现状，提出了同时考虑高炉配罐制度和铁水包备包的铁水包周转数的计算模型，应用模型计算了重钢新区铁水包周转数，研究了铁水包周转数的优化方法，得到以下结论：
(1) 铁水包周转数由工艺要求周转所需数、备包数及配罐富裕数组成.
(2) 优化铁水包周转数的关键在于优化空包和重包缓冲容量，实际生产中可采取优化高炉配罐制度和连浇炉数的生产措施，两座高炉-两座转炉模式下，模型计算的单一优化配罐制度及连浇炉数均可减少2 个铁水包，联合优化配罐制度和连浇炉数可减少4 个铁水包.
参 考 文 献：
[1] 殷瑞钰. 冶金流程集成理论与方法 [M]. 北京：冶金工业出版社，2013: 230-231.
Yin R Y. Theory and Method of Metallurgical Process Integration[M]. Beijing: Metallurgical Industry Press, 2013: 230−231.
[2] 李金柱，王飞，杨春政. 首钢京唐铁水包多功能化应用实践 [J].炼钢，2014, 30(4): 61-64.
Li J Z, Wang F, Yang C Z. Practice of Multi-functional Hot MetalLadle Technology in Shougang Jingtang [J]. Steelmaking, 2014,30(4): 61−64.
[3] 叶薇，邹忠平，苏莉，等. 重钢铁水运输“一罐制”工艺设计 [J].炼铁, 2012, 31(2): 21-24.
Ye W, Zou Z P, Su L, et al. One Ladle from BF to BOF ProcessDesign for Hot Metal Transportation in Chongqing Iron and SteelCo., Ltd. [J]. Ironmaking, 2012, 31(2): 21-24.
[4] 黄帮福，贺东风，田乃媛，等. 鱼雷罐的运行控制 [J]. 北京科技大学学报，2010, 32(7): 933-937.
Huang B F, He D F, Tian N Y, et al. Operational Control of TorpedoLadles [J]. Journal of University of Science and Technology Beijing,2010, 32(7): 933-937.
[5] 韩伟刚，郦秀萍，施一新，等. 基于排队论“一包到底”模式的在线铁水包数量 [J]. 钢铁，2013, 48(5): 21-24.
Han W G, Li X P, Shi Y X, et al. Online Ladle Quantity of “Oneopen-ladle-from-BF-to-BOF” Route by Using Queuing Theory [J].Iron and Steel, 2013, 48(5): 21-24.
[6] Liang S, Wang J, Wang H, et al. Simulation and Optimization ofMaterial Flow System for “the mode of one open ladle” in BF-BOFRegion [C]//Computer Science and Education (ICCSE), 7thInternational Conference on IEEE. 2012: 716-720.
[7] 王峰. 高炉-连铸机区段的精准设计和生产调控 [D]. 北京：北京科技大学，2011: 95-101.
Wang F. Precise Design and Production Control of Blast Furnace–Continuous Caster Section [D]. Beijing: University of Science andTechnology Beijing, 2011: 95-101.
[8] 杨楚荣. “一罐到底”铁水运输工艺铁水罐配置的优化分析 [C]//中国金属学会，宝钢集团有限公司. 第十届中国钢铁年会暨第六届宝钢学术年会论文集. 2015: 1-5.
Yang C R. Quantity Optimization and Analysis of Hot Metal Ladlefor “Common Ladle System” Hot Metal Transportation [C]//TheChinese Society for Metals, Baosteel Co. Proceedings of the 10thCSMS Steel Congress & 6th Baosteel Biennial AcademicConference. 2015: 1-5.
[9] 郑忠. 炼钢连铸的生产运行控制- 计划调度技术及应用[C]//2015 年全国炼钢-连铸过程协同优化学术研讨会论文集.2015: 172-188.
Zheng Z. Production Running Control of Steelmaking andContinuous Casting Process-Planning and Scheduling Technologyand Its Application [C]//2015 National Symposium on SynergyOptimization of Steelmaking and Continuous Casting. 2015: 172-188.
[10] 蔡峻，汪红兵，贺东风，等. 钢厂钢包周转率的影响因素 [J]. 北京科技大学学报, 2013, 35(8): 1072-1079.
Cai J, Wang H B, He D F, et al. Affecting Factors of the TurnoverRate of Steel Ladle in Steelmaking Plants [J]. Journal of Universityof Science and Technology Beijing, 2013, 35(8): 1072-1079.
[11] 蔡峻，贺东风，汪红兵，等. 基于浇次计划的钢包周转数量计算模型 [J]. 重庆大学学报，2013, 36(11): 59-65.
Cai J, He D F, Wang H B, et al. Calculation Model for the TurnoverNumber of Steel Ladle Based on Casting Schedule [J]. Journal ofChongqing University, 2013, 36(11): 59-65.
[12] 黄帮福，施哲，朱红波，等. 基于甘特图的钢包运行控制模型研究 [J]. 中南大学学报(自然科学版), 2014, 45(7): 2164-2170.
Huang B F, Shi Z, Zhu H B, et al. Operational Control Model of SteelLadle Based on Gantt Chart [J]. Journal of Central South University(Natural Science Edition), 2014, 45(7): 2164-2170.
[13] 黄帮福，田乃媛，施哲，等. 钢包互用条件及影响因素 [J]. 重庆大学学报，2017, 40(2): 52-59.
Huang B F, Tian N Y, Shi Z, et al. Precondition and Influence Factorsof Steel Ladle Interaction [J]. Journal of Chongqing University, 2017,40(2): 52-59.
[14] 冯凯，贺东风，徐安军，等. 基于钢包运行稳定性的炼钢厂生产计划优化 [J]. 东北大学学报(自然科学版), 2015, 36(11): 1619-1623.
Feng K, He D F, Xu A J, et al .Optimization of Production ScheduleBased on Ladle Running Stability in Steel Plant [J]. Journal ofNortheastern University (Natural Science Edition), 2015, 36(11):1619-1623.
[15] 王学阳，徐安军，贺东风，等. 基于Plant Simulation 的炼铁厂物流仿真优化 [J]. 钢铁研究，2017, 45(1): 17-22.
Wang X Y, Xu A J, He D F, et al. Simulation Optimization ofLogistics for Iron-making Plant Based on Plant Simulation [J].Research on Iron and Steel, 2017, 45(1): 17-22.
[16] 芦永明，王丽娜，陈宏志，等. 考虑生产组织约束的钢铁企业合同计划 [J]. 重庆大学学报，2012, 35(11): 86-91, 110.
Lu Y M, Wang L N, Chen H Z, et al. Order Planning for Iron andSteel Enterprise Considering Production Organization Constraints[J]. Journal of Chongqing University, 2012, 35(11): 86-91, 110.
[17] 周炳海，余佳迪，邵健一. 基于可用度评价的串行生产线缓冲分配方法 [J]. 浙江大学学报(工学版), 2015, 49(5): 893-900.
Zhou B H, Yu J D, Shao J Y. Buffer Allocation Method for SeriesProduction Lines Based on Availability Assessments [J]. Journal ofZhejiang University (Engineering Science), 2015, 49(5): 893-900.
[18] Papadopoulos H T, Vidalis M I. A Heuristic Algorithm for the BufferAllocation in Unreliable Unbalanced Production Lines [J].Computers and Industrial Engineering, 2001, 41(3): 261-277.