马 柯1,贾为征2,刘国峰2,韩立鹏2
(北京首钢自动化信息技术有限公司京唐运行事业部,河北 唐山 063200)
摘要:收集了冷轧产线立式加热炉带钢温度控制下的数据集,该数据集包含有带钢温度、厚度、宽度、运行速度、带钢长度、功率。通过python语言搭建机器学习模型,对数据集进行学习、建模,通过影响因素来预判带钢实际温度,并通过均方根误差来判定模型的精度。
关键词: 带钢温度;均方根误差;机器学习;LightGBM算法
0 引言
退火炉加热模型计算中,对于带钢进入炉区温度的预判及其重要,精度高的预判能够提供一个更精准的加热策略,来满足生产工艺需求,从而减少热瓢曲现象的发生[1]。目前产线应用较多的加热模型,依靠实时的测量值和带钢的物性实时地计算/预测带钢在各段出口的温度,使用了基于物理热交换(对流换热,辐射换热)的数学模型。本文针对镀锌产线立式加热炉,我们收集了大量数据集[2],采用python及其机器学习生态系统,对数据集分析,建模,来完成带钢在加热区域出口温度实际值的预判[3]。通过均方根误差计算,来验证模型的好坏。
1 数据集
数据集为镀锌产线立式加热炉,辐射管加热段,利用带钢温度控制模式下数据,产线运行速度不为0。带钢厚度在0.5~1.5 mm之间,带钢速度为1~130 m/min的炉区加热数据,另外包含带钢长度、带钢温度、功率实际值。数据集是13 249×9的一个二维数组,部分数据见表1。表中:number为序列号,Thick为带钢厚度,Width为宽度,Length为长度,Spd_mea速度测量值,ST_mea加热段出口处带钢温度测量值, PoAvg_mea加热段平均功率值,TTsAvg_mea加热段区域温度测量值,ST_est热模型计算出的加热段出口段温度,ST加热段入口处带钢温度测量值。
表1 数据集示例
|
number |
Thick/ mm |
Width/mm |
Length/mm |
Spd_mea/(m·min-1) |
ST_mea/℃ |
TTsAvg_mea/℃ |
PoAvg_mea/% |
ST_est/℃ |
ST/℃ |
|
1 |
0.575 |
1224 |
3549 |
130 |
790 |
839 |
63 |
794 |
190 |
|
2 |
0.575 |
1224 |
3539 |
130 |
790 |
839 |
63 |
794 |
190 |
|
3 |
0.575 |
1224 |
3527 |
130 |
790 |
839 |
63 |
794 |
189 |
|
4 |
0.575 |
1224 |
3516 |
130 |
790 |
839 |
63 |
794 |
190 |
|
5 |
0.575 |
1224 |
3516 |
130 |
790 |
839 |
63 |
794 |
189 |
2 目标和评估指标
目标是利用测试集中可用的信息,来预测带钢经过辐射管加热段后的实际温度。评估指标为,利用均方根误差(root mean squared error, RMSE)来评价模型的好坏[4]。其数学公式为

当均方根误差越小时,表示数据的拟合效果越好,测试值越接近实际值。
3 分析数据
为了对数据集每一个字段进行观察,采用绘制箱式图的方式来得到数据字段的分布。采用Python语言,利用数据可视化相关库完成,导入matplotlib、seaborn、numpy、pandas,进行绘制,输出结果如图1所示。通过图1能够直观了解到每个字段的分布情况。

图1 特征值箱式图
绘制各个数值特征之间的相关矩阵热图[5],来理解目标变量如何受数值特征影响,绘制 ST_mea 与 ["Thick", "Width", "Length", "Spd_mea", "PoAvg_mea", "TTsAvg_mea","ST","ST_est","ST_mea"]之间的相关矩阵热图,如图2所示。通过特征值之间相关矩阵热图,能够得到特征值对带钢温度影响程度,影响程度从大到小依次为PoAvg_mea、Spd_mea、ST、 TTsAvg_mea、Thick、Length、Width。另外,Spd_mea和Thick、Length、Width有很强的相关性[6],ST_est为加热模型计算出的实际温度,不用于建模,可用于对比拟合精度。
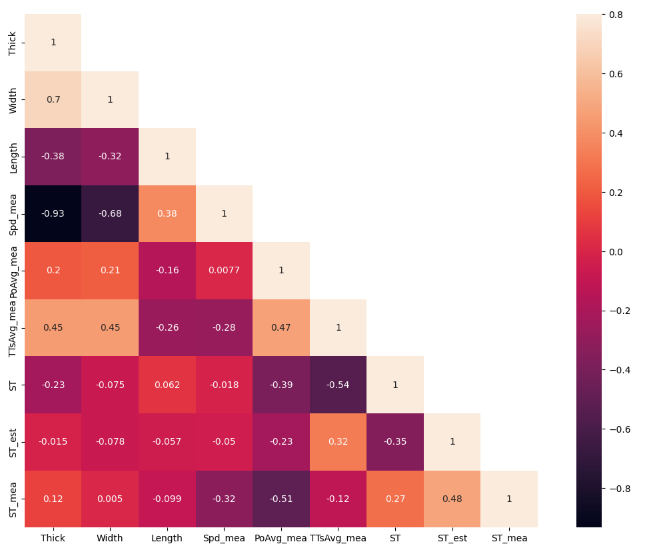
图2 特征值相关矩阵热图
4 模型的建立与求解
首先,准备好数据,训练集数据为data_train,X_train包含了PoAvg_mea、Spd_mea、ST、 TTsAvg_mea、Thick、Length、Width这几个特征,Y_train为ST_mea。测试集数据为data_test, X_test包含了测试集数据PoAvg_mea、Spd_mea、ST、 TTsAvg_mea、Thick、Length、Width,y_test为测试集数据ST_mea。部分代码如下:

定义评价函数,实现均方根误差的计算,引用Numpy库,pandas库、 calendar库完成计算,部分代码如下:

为了训练出高精度的模型,引入LightGBM算法,LightGBM是微软开发的boosting集成模型,LightGBM作为常见的强大Python机器学习工具库,具有以下优点:更快的训练效率,低内存使用,更高的准确率,支持并行化学习,可处理大规模数据,支持直接使用 category 特征。面对工业级海量的数据,普通的 GBDT 算法无法满足需求。 LightGBM解决能够解决大数据量级下的 GBDT 训练问题,以便工业实践中能支撑大数据量并保证效率[7]。
引入机器学习lightgbm库,对数据集进行拟合训练,利用训练结果进行测试集计算,将结果利用均方根计算误差[8],代码如下:
通过对数据集X_train, y_train经过LightGBM模型的训练,得到的计算模型去求解X_test值[9],最终得到y_pred就是通过模型计算出的测试集带钢在出口时的实际温度。通过均方根误差计算,误差为0.007787,同样我们对热模型求出的温度实际值和温度测量值进行均方根误差计算,得到的结果时0.013 096。输出结果见表2。
表2 误差统计表
|
模型 |
RMSLE |
|
hot-mod |
0.013 096 |
|
LightGBM |
0.007 787 |
5 结语
利用Python机器学习进行建模得到的结果,精度在这种情况下大于热模型的计算结果。在进行炉子建模过程中,可以将机器学习模型纳入计算过程中,结合热模型,以及PID算法,能够实时对模型计算结果进行调节,以达到理想的精度[10]。
参考文献
[1] 路佳佳.基于集成特征选择和随机森林的古代玻璃分类模型[J/OL].硅酸盐学报:1-6[2023-03-15].https://doi.org/10.14062/j.issn.0454-5648.20220790.
[2] 刘玉敏,赵哲耘.基于特征选择与SVM的质量异常模式识别[J/OL].统计与决策,2018(10):47-51[2023-03-15].https://doi.org/10.13546/j.cnki.tjyjc.2018.10.010.
[3] 徐小青,郝晓东,周石光,等.热镀锌退火过程中的温度控制策略[J].钢铁研究学报,2016,28(1):44.
[4]杨枕,任伟超,李洋龙,等.连续退火炉二级管温模型优化[J].冶金自动化,2018,42(4):40.
[5] 揣雪雨. 基于LightGBM算法的个人信用评估模型研究[D]. 郑州:郑州大学,2020.
[6]郭英,陈垒.连续退火炉带钢温度数学模型开发及应用[J].冶金能源,2021,40(06):28.
[7] 邢长征,徐佳玉.LightGBM混合模型在乳腺癌诊断中的应用[J/OL].计算机工程与应用:1-10[2023-03-15].
[8] 张笑宇,沈超,蔺琛皓等.面向机器学习模型安全的测试与修复[J/OL].电子学报,2022(12):2884
[9] 周书蔚,杨冰,王超等.机器学习法预测不同应力比6005A-T6铝合金疲劳裂纹扩展速率[J/OL].中国有色金属学报:1-17[2023-03-15].
[10] 李赞. 异构数据集下通信高效的联邦学习算法研究[D].合肥:中国科学技术大学,2022.
